Hex grid in single integer

AZsPCs: AP Math

Al Zimmermann hosts awesome Programming Contests every once in a while. They usually run for a long time (multiple months) and it allows mathematicians and programmers to compete in optimization problems. Usually the search space is very large and optimal solutions aren’t found for large N-values.

This time the contest was called “AP Math” and the goal was:

Given a hexagonal grid of size N, select the maximum amount of cells so no three cells form an arithmetic progression.

During this contest I didn’t find the right way to attack the problem, but I did discover a clever way to store all the hex coordinates in a singe integer value and do the math on that; which I wanted to share here.

Arithmetic progression?

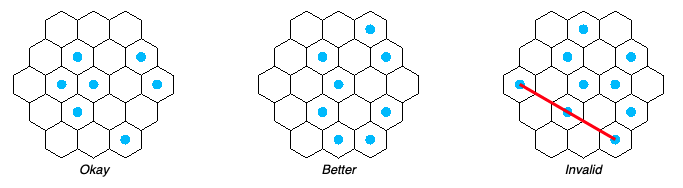
The main goal in the contest is to select cells in a hex grid with this one rule “no three cells form an arithmetic progression”.

What does this mean? If you look at the example above for a N=3 hex grid you can see that we have to select cells, with the rule that no two points can have another cell in between, on the mid point.

Look at this website for more examples and a complete description: AP Math.

So to find solutions, we need a way to store the coordinates of this hex grid and a way to determine given two cells, which other cells are illegal.

Storing coordinates as single 32-bit integer

There are multiple ways to store the coordinates of an hexagonal grid. The best write-up I’ve found is located at redblobgames.com. I’m using an axial grid, so each coordinate has an x and y value.

But instead of working with an x and y value, I’m storing each coordinate as a single 32-bit integer.

To generate all of them I used the following (Java) code:

int N = 11;
int S = N + N - 1;

Set<Integer> indexes = new HashSet<>();
// Generate all hex points: (as single int)
for(int x = 0; x < S; x++) {
    for(int y = 0; y < S; y++) {
        // Cut off the two triangular edges to make a hex grid:
        if(x+y >= (N-1) && x+y < (3*N - 2)) {
            indexes.add(x << 16 | y);  //<-- store all the positions x, y both into a single integer value.
        }
    }
}

As you can see, I’m storing x and y in a single integer value, shifted 16 bits.

Now you might ask: how is storing each coordinate as a single 32-bit value useful? What does it add?

Well, suppose we have two coordinates from the complete list of all hex grid coordinates mentioned above. With these two indexes in our hex grid we can do the following:

// A bitmask to check for even numbers
int BOTH_EVEN_MASK = 1 << 16 | 1;

if (((index1 ^ index2) & BOTH_EVEN_MASK) == 0) {
    // Points index1 and index2 has the following midpoint:
    int invalidMid = (index1 + index2) >> 1;
}

int invalid1 = (index2 << 1) - index1;
int invalid2 = (index1 << 1) - index2;

Using very limited control code and little math we can calculate all three points that are needed for this contest. Given just the two coordinates we get the two or three points that are invalidated. This is much faster than any other coordinate system I tried. A single subtract of two indexes gives the x and y of the new point: less work for the CPU.

Turns out, I didn’t even need to use the actual x and y values anywhere, I could stay in this coordinate-system while searching. If you want to though, just mask and shift:

int x = index >>16 & 0xFFFF;
int y = index & 0xFFFF;

This was my little ‘hack’ for this contest. I might be able to use this xy as a single integer on more occasions, in other contests. It’s a nice tool to have in the toolbox.