Update Apr 22, 2016: I’ve made a video which explains most of what is in this blogpost:

Two standards

Yes, this blogpost is about paper. This has absolutely nothing to do with programming, but there is a beautiful piece of math involved.

There are two major standards of paper sizes in the world. The most widely used is ISO-216, more commonly known as the A-series, as in ‘A4’ size. This system is used almost everywhere in the world, the main exceptions are United States and Canada. In the United States they use their own US Letter standard.

US Letter

The standard US Letter has a size of: 216 mm x 279 mm (8.5 by 11 inches) and a ratio of 1,291666666666667.
(I’ll explain why this ratio is important in the math part below!).

The origin of this size is very vague and lost in history. Most origins say (from Wikipedia):

The 11” length of the standard paper being about a quarter of “the average maximum stretch of an experienced vatman’s arms.”

Basically US Letter is a standard because it is a standard, don’t ask questions, just deal with it.

ISO-216, the A-standard

The letter size of the ISO standard is A4. The size is 210 mm × 297 mm and has a ratio of √2 (math!).

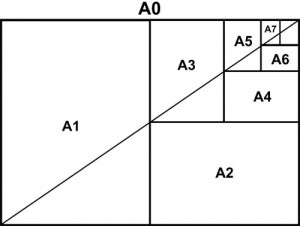
The ratio is what makes this standard superior. This of course isn’t a coincidence. Smart people have thought about these sizes, it became a standard because it was superior. The ‘magic’ property A4 paper size has is that is consists of exactly two A5 papers side-by-side. In turn, two of these A4 papers make up the larger A3 paper. This makes it very easy for example to make a booklet in A5 format consisting of folded A4 papers. Also if you scale up a document in A5 it’ll exactly fit A4. If you want to use a copier and print two A5 pages on A4 paper, go ahead! This is impossible to do with US Letter, you’ll end up with white spaces or stretched documents!

Aspect ratio math

How does this work mathematically? The magic hides in the fact that 2 / √2 = √2. Imagine we have a piece of paper with long side A and short side B. If we fold the long side and create a new paper size with B and C, what is the aspect ratio?

Given:
A/B = √2 (aspect ratio)
C = A/2 (new short length is A folded in half)

So what is the new aspect ratio of B/C?
B/C = B/(A/2)

B/(A/2) = 2/(A/B)

2/(A/B) = 2/√2

2/√2 = √2!

When you start with the aspect ratio of √2, the resulting folded aspect ratio is again √2. You can keep doing this.

Lets take the largest standard paper size, A0: 841 × 1189. What happens when we fold it? Well: 841 becomes the long side, 1189/2=594.5 the short side. This is indeed the A1 paper size (594 mm x 841 mm). It will keep the magic √2 aspect ratio!

Size of A0 paper

Now that we can explain the aspect ratio, we still don’t know how we ended up with the magic numbers 210 mm × 297 mm. This number originates simply because the A0 paper size is defined as having an aspect ratio of √2 and a surface area of 1 m2.

This is all you need to know, √2 and 1m2.

Given:
A*B = 1m2 = 1000² (our paper size)
A/B = √2 (our ratio)

The first formula we need is:

area = (diagonal²) / (ratio + (1/ratio))

When we plug in the given values:
1000² = (diagonal²) / (√2 + (1/√2))

diagonal² = (√2 + (1/√2)) × 1000² ≅ 2121320.34

Remember our magic aspect ratio: 
A / B = √2:
B = A × √2

With our old pal Pythagoras we now know:
diagonal² = A² + B² (= 2121320.34)

Let's get rid of B²:
diagonal² = A² + (A * √2)²

Now we can simplify:
diagonal² = A² + (A × √2)²
diagonal² = A² + 2 × A²
diagonal² = 3 × A²

And easily calculate the result:
3 × A² = 2121320.34

A = √(2121320.34 / 3) ≅ 840.89
B = A × √2 ≅ 1189.20

We started with just two simple numbers, ratio: √2 and area: 1m2 and now we’ve ended up with the A0 paper, 841 mm and 1189 mm!
To calculate the rest of the A-series you just take:

A' = B / 2
B' = A

Mathematically folding it in half results in: 594 mm x 841 mm = exactly the A1 paper size!

Keep on folding

When we take an A4 paper and keep folding it, we get the following aspects (aspects fluctuate a little bit due to rounding):

A4	210 mm × 297 mm ratio: 1.414
A5	148 mm × 210 mm ratio: 1.419
A6	105 mm × 148 mm ratio: 1.409
A7	74  mm × 105 mm ratio: 1.418
A8	52  mm × 74  mm ratio: 1.423
A9	37  mm × 52  mm ratio: 1.405
A10	26  mm × 37  mm ratio: 1.423

But what do you end up with folding the US Letter? Let’s see:

216 mm x 279 mm ratio: 1.291
139 mm x 216 mm ratio: 1.554 <- What?
108 mm x 139 mm ratio: 1.287 <- Ah..
69  mm x 108 mm ratio: 1.565 <- HUH!?
54  mm x 69  mm ratio: 1.278
34  mm x 54  mm ratio: 1.588
27  mm x 34  mm ratio: 1.259 <- Oh god...

This fluctuating ratio results in so much wasted space, ink, paper! And it is just ugly! If you decide to scale something up from A5 to A4 it instantly fits, if you scale something in US Letter… you’ll either have to crop or stretch or leave unprinted paper.

US Letter is bad for the environment!

Ban the US Letter standard, hurray for math!