An amazing website I keep running into (especially through Hacker News) is: Red Blob Games.

It has a lot of amazing algorithms explained using interactive Javascript examples. For example take a look at how Amit explains Hexagonal grids and A* pathfinding. The interactive demo’s make it easy to grasp all these fun algorithms and implement them yourself.

Pathfinding for Tower Defense

Last week though I was reading this tutorial, Pathfinding for Tower Defense.

He explains a method for creating a single vector/flow field for game AI’s to follow. This allows a single calculation to be used by a lot of AI bots, which is great for a Tower Defense game.

A new game…

However, when I was playing with the bottom Javascript example (after pressing ‘Start animation’) I found myself playing a new little game of my own. There is a box, 20x10 where you can place walls, also you are able to drag/move the start position around.

The goal:

“What is the longest path possible? / What is the highest number I can reach?”

After I found out I can move the start position around, I came up with the following configuration:

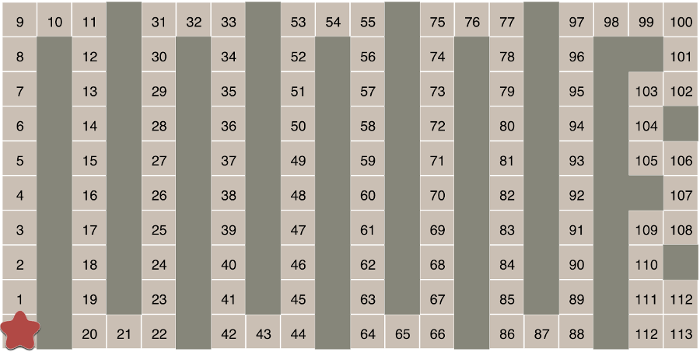
The maze is 113 long… but it turns out this is far from optimal. After coding up a little solver and playing around I found the following configuration:

This is a solution that goes up to 124 (near the top left corner). I’ve also found one later with a score of 125.

It seems that diagonals are the best way to pack the longest maze into there, but the problem is, one diagonal cuts the field in two smaller parts. Zig-zagging works great, but there is no ‘easiest’ way to zig-zag.

It doesn’t seem to me that there is a trivial solution? I haven’t found one at least, is there? Are there simple optimal patterns for given boxes, NxN?

Searching for a solution seems to be NP-hard and even 20x10 is out of the question, the amount of possible configurations of walls and starting positions is huge and grows exponentially. Coding up a solver is pretty easy though, using some simple heuristics and some random searches I got my 125 solution.

Maybe this would be a fun puzzle for a future AZsPCs contest…?

Can you get a better configuration than 125? I’d love to know.

Neighbors algorithm

When I wrote a score checker for the puzzle above I needed a way to get the neighbors in an 2D array. I’ve gotten used to code 2D mazes/puzzles and I always use the following way to calculate all the neighbors.

I find this to be easier and more readable that the alternatives, going over all the -1/+1 combinations or having two nested loops.

// We have a 2D maze:
int[][] maze = new int[10][20];

// And a certain location, row and column:
int row = 8;
int col = 10;

// List all neighbors:
for(int direction = 0; direction < 9; direction++) {
    if(direction == 4) continue; // Skip 4, this is ourself.
    
    int n_row = row + ((direction%3) - 1); // Neighbor row
    int n_col = col + ((direction/3) - 1); // Neighbor column

    // Check the bounds:
    if(n_row >= 0 && n_row < maze.length && n_col >= 0 && n_col < maze[0].length) {
        
        // A valid neighbor:
        System.out.println("Neighbor: " + n_row + "," + n_col + ": " + maze[n_row][n_col]);
    }
}

How does this work?

First we list all directions with a single integer, 0 to 9, and we’ll need to skip the middle number four, this points to ourself.

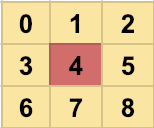
From this single direction we’re able to easily calculate both the new row value (n_row) and the new col value (n_col). To do this we’ll need to divide by three and use modulo three.

Neighbor row value:

To find the new row value we start our by using modulo 3. The only thing left to do is to subtract 1 and we’ll get the new row value for each direction:

int n_row = row + ((direction%3) - 1);

Neighbor col value:

The same thing can be done for the col value. Instead of using modulo 3, we’ll be using divide by 3. And the same as with the row value, we’ll also need to subtract 1 to get the following new column values:

int n_col = col + ((direction/3) - 1);

And there you go, list all neighbors in a 2D array without using two nested loops and dirty checks.

Happy coding!